Théorème du point fixe de Brouwer

Vous lisez un « bon article » labellisé en 2009.

Pour les articles homonymes, voir De Brouwer.

En mathématiques, et plus précisément en topologie algébrique, le théorème du point fixe de Brouwer fait partie de la grande famille des théorèmes de point fixe, qui énoncent que si une fonction continue f vérifie certaines propriétés, alors il existe un point x₀ tel que f(x₀) = x₀. La forme la plus simple du théorème de Brouwer prend comme hypothèse que la fonction f est définie sur un intervalle fermé borné non vide I et à valeurs dans I. Sous une forme plus générale, la fonction est définie sur un convexe compact K d'un espace euclidien et à valeurs dans K.

Si, parmi les centaines de théorèmes de point fixe^[1], celui de Brouwer est particulièrement célèbre, c'est en partie parce qu'il est utilisé dans de nombreuses branches mathématiques. Dans sa branche d'origine, ce résultat est l'un des théorèmes clés caractérisant la topologie d'un espace euclidien, comme le théorème de Jordan, celui de la boule chevelue ou de Borsuk-Ulam^[2]. À ce titre, il est un des théorèmes fondamentaux de la topologie^[3]. Ce théorème intervient aussi pour établir des résultats fins sur les équations différentielles ; il est présent dans les cours élémentaires de géométrie différentielle. Il apparaît dans des branches plus inattendues, comme la théorie des jeux, où John Nash l'utilise^[4] pour montrer l'existence d'un équilibre pour un jeu de n personnes avec stratégies mixtes. Historiquement, le théorème est étudié à la suite de travaux sur les équations différentielles de mathématiciens français comme Poincaré et Picard. Démontrer des résultats comme le théorème de Poincaré-Bendixson demande l'usage d'outils de topologie. Ces études de la fin du XIX^e siècle débouchent sur plusieurs versions successives du théorème ; en 1912, Luitzen Egbertus Jan Brouwer en propose une démonstration générale, établissant à nouveau un résultat déjà prouvé par Hadamard en 1910.

Énoncés

Il existe plusieurs formes du théorème, selon le contexte d'utilisation. La plus simple est parfois donnée sous la forme suivante :

Il est possible de généraliser à toute dimension finie.

De manière équivalente^{[Note 1]} :

On trouve une forme encore plus générale, mais habituellement, elle porte alors un autre nom :

Approche intuitive

Commentaires attribués à Brouwer

L'origine de ce théorème proviendrait de l'observation d'une tasse de café par Brouwer^{[Note 2]}. Quand on mélange son sucre, il semble qu'il y ait toujours un point immobile. Il en déduit que : « À tout moment, il y a un point de la surface qui n'aura pas changé de place »^[7]. Le point fixe n'est pas nécessairement celui qui semble immobile car le centre du tourbillon bouge un petit peu. Le résultat n'est pas intuitif, car le point initialement fixe aura peut-être bougé, mais un autre point fixe apparaîtra.

Brouwer aurait ajouté : « Je peux formuler ce magnifique résultat autrement, je prends une feuille horizontale, une autre feuille identique que je froisse et que je replace en l'aplatissant sur l'autre. Un point de la feuille froissée est à la même place que sur l'autre feuille »^[7]. Quand Brouwer aplatit sa feuille froissée, il ne la déplie pas, il l'écrase, comme à l'aide d'un fer à repasser.

Dimension un

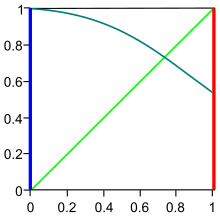
En dimension un, le résultat est à la fois intuitif et aisé à démontrer. On note ${\displaystyle {\mathopen {[}}a\,;b{\mathclose {]}}}$ le domaine de définition de ${\displaystyle f}$. La fonction ${\displaystyle f}$ est continue et à valeurs dans le même segment. Dire que cette fonction ${\displaystyle f}$ admet un point fixe, revient à dire que son graphe (en bleu-gris sur la figure de droite et choisi dans ce cas égal à celui de la fonction cosinus sur l'intervalle ${\displaystyle {\mathopen {[}}0\,;1{\mathclose {]}}}$) croise celui de la fonction définie sur ${\displaystyle {\mathopen {[}}a\,;b{\mathclose {]}}}$, qui à ${\displaystyle x}$ associe ${\displaystyle x}$ (en vert sur la figure de droite).

Intuitivement, une ligne (en noir) qui part d'un côté d'un carré (en bleu) pour rejoindre le côté opposé (en rouge) croise nécessairement les diagonales et en particulier la verte sur la figure.

Une démonstration n'est pas difficile à établir. Considérons la fonction continue ${\displaystyle x\mapsto f(x)-x}$. Elle est positive en ${\displaystyle a}$ et négative en ${\displaystyle b}$. Le théorème des valeurs intermédiaires assure qu'elle possède un zéro dans ${\displaystyle {\mathopen {[}}a\,;b{\mathclose {]}}}$. Ce zéro est un point fixe de ${\displaystyle f}$.

Brouwer aurait exprimé ce résultat de la manière suivante : « Au lieu d'examiner une surface, nous allons montrer le théorème sur un bout de ficelle. Partons d'un état de la ficelle bien dépliée, puis replions-la. Écrasons la ficelle repliée. Là encore un point de la ficelle n'a pas changé de place par rapport à sa position initiale sur la ficelle non repliée. »^[7].

Dimension deux

En dimension deux, si K, le domaine de définition de f est d'intérieur vide, c'est un segment. Sinon, K est « semblable » à une boule unité fermée de R², pour une norme arbitraire^{[Note 1]}. Le terme « semblable » signifie qu'il existe un homéomorphisme φ de la boule unité vers K. En notant h l'application continue φ⁻¹∘f∘φ de la boule unité dans elle-même, les points fixes de f sont exactement les images par φ des points fixes de h. Autrement dit, on peut sans perte de généralité supposer que K est la boule unité fermée, pour la norme qui associe à tout vecteur du plan la plus grande valeur absolue de ses deux coordonnées, c'est-à-dire que K est l'ensemble [–1, 1]×[–1, 1].

Si l'on définit la fonction g comme celle qui à x associe h(x) – x, un point fixe de h est un point de [–1, 1]×[–1, 1] en lequel la fonction g atteint le vecteur nul, c'est-à-dire en lequel les deux composantes g₁ et g₂ de g s'annulent simultanément.

La suite de ce paragraphe semble contenir un travail inédit ou des déclarations non vérifiées (octobre 2013).

Vous pouvez aider en ajoutant des références ou en supprimant le contenu inédit. Voir la page de discussion pour plus de détails.

Un « raisonnement » intuitif incite à penser que l'existence d'un tel point est plausible : la fonction g₁ est une fonction de [–1, 1]×[–1, 1] dans R. Elle peut s'interpréter comme une carte d'une région, qui en chaque point donne l'altitude (illustrée sur la première figure à droite). Sur la zone {–1}×[–1, 1], cette altitude est positive (en rouge sur la figure), en revanche sur {1}×[–1, 1], elle est négative (en bleu sur la figure). Ceci « laisse penser que » la « courbe » de niveau 0 est une ligne (en vert sur la figure) qui part d'un point [–1, 1]×{1} pour finir sur un point de [–1, 1]×{–1}, mais cette intuition est fausse : la zone verte n'est pas nécessairement une ligne ni même une partie connexe. Le même « raisonnement » appliqué à g₂ « laisse penser que » la courbe de niveau 0 serait cette fois-ci une ligne partant d'un point de {–1}×[–1, 1] pour terminer sur un point de {1}×[–1, 1] (illustré sur la deuxième figure, la ligne est en jaune).

L'« évidence » intuitive que ces deux hypothétiques « lignes » de niveaux (en vert et en jaune) doivent nécessairement se croiser (ce point de croisement étant alors un point fixe de h) est donc une fausse piste.

Dimension finie

Le paragraphe précédent se généralise à toute dimension finie, autant dans son raisonnement rigoureux du début que dans ses fausses intuitions de la suite.

Illustrons ces dernières en dimension 3. L'objectif est toujours de tenter de se persuader à peu de frais de la véracité du théorème de Poincaré-Miranda, c'est-à-dire de l'existence d'un zéro de la fonction g, qui maintenant possède trois coordonnées.

La suite de ce paragraphe semble contenir un travail inédit ou des déclarations non vérifiées (octobre 2013).

Vous pouvez aider en ajoutant des références ou en supprimant le contenu inédit. Voir la page de discussion pour plus de détails.

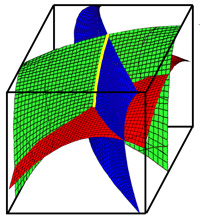
La première coordonnée est positive sur la face gauche du cube et négative sur la face droite. « Il y a tout lieu de penser que » la zone des zéros contient une « nappe », illustrée en bleu sur la figure de droite. Cette « nappe » couperait le cube en au moins deux composantes connexes, l'une contenant une portion de la face de droite l'autre celle de gauche. Si l'axe des y décrit la direction « devant-derrière » le même « raisonnement » « laisse penser à » l'existence d'une « nappe », en vert sur la figure, qui couperait encore en au moins deux composantes connexes le cube. L'intersection des deux « nappes » contiendrait « probablement » une « ligne », en jaune sur la figure, partant de la face du haut pour rejoindre celle du bas. La troisième composante de g décrirait, cette fois-ci, une « nappe » en rouge sur la figure. Cette « nappe » « semble » croiser « nécessairement » la ligne jaune. Ce point d'intersection serait un point fixe recherché.

Fragments d'histoire

Préhistoire

Comprendre la préhistoire du théorème du point fixe de Brouwer impose un passage par une équation différentielle. À la fin du XIX^e siècle, une vieille question^[8] focalise à nouveau l'attention de la communauté mathématique, celle de la stabilité du système solaire^[9]. La résoudre suppose la mise au point de nouvelles méthodes. Comme le fait remarquer Henri Poincaré, qui étudie le problème des trois corps, la recherche d'une solution exacte est vaine : « Rien n’est plus propre à nous donner une idée de la complication du problème des trois corps et en général de tous les problèmes de Dynamique où il n’y a pas d’intégrale uniforme et où les séries de Bohlin sont divergentes »^[10]. Ce mathématicien remarque aussi que la recherche d'une solution approchée n'est pas plus efficace : « plus nous cherchons à obtenir des approximations précises et plus le résultat va diverger vers une imprécision croissante »^[11].

Il étudie une question analogue à celle du mouvement de la surface d'une tasse de café. Que peut-on dire, en général, des trajectoires d'une surface animée par un courant constant^[12] ? Poincaré découvre que la réponse réside dans ce que l'on appelle maintenant les propriétés topologiques de la zone contenant la trajectoire. Si cette zone est compacte, c'est-à-dire à la fois fermée et bornée, soit la trajectoire s'immobilise, soit elle s'approche de plus en plus d'une boucle qu'elle parcourt indéfiniment^{[Note 3]}. Poincaré va plus loin, si la zone est de même nature que celle d'un disque, comme c'est le cas pour la tasse de café, il existe nécessairement un point fixe. Ce point fixe est invariant par toutes les fonctions qui, à chaque point de la surface initiale, associent sa position au bout d'une période t. Si cette zone correspond à une bande circulaire ou si elle n'est pas fermée^{[Note 4]}, ce n'est pas nécessairement le cas.

Pour mieux comprendre l'équation différentielle, une nouvelle branche des mathématiques voit le jour. Poincaré l'appelle l'analysis situs, l'Encyclopædia Universalis la définit comme celle qui « concerne les propriétés invariantes d’une figure lorsqu’on la déforme de manière continue quelconque, sans déchirure (par exemple, dans le cas de la déformation de la sphère, les propriétés corrélatives des objets tracés sur sa surface »^[13]. Dès 1886, Poincaré établit un résultat^[14] dont on sait aujourd'hui qu'il équivaut au théorème du point fixe de Brouwer^[15]. Un peu plus tard, il développe l'un des outils de base pour mieux comprendre l'analysis situs, que l'on appelle maintenant le groupe fondamental ou le groupe de Poincaré^[16]. Cette méthode est utilisée dans une des démonstrations du théorème présentées dans l'article^{[Note 5]}.

Par certains côtés, l'approche de Poincaré est analogue à celle d'Émile Picard, un mathématicien contemporain qui généralise le théorème de Cauchy-Lipschitz^[17]. La démarche de Picard s'appuie sur un résultat qui sera formalisé plus tard par un autre théorème du point fixe, dit de Banach. Ce théorème ne s'appuie pas sur les propriétés topologiques du domaine de définition, mais sur le fait que la fonction étudiée est contractante.

Premières démonstrations

À l'aube du XX^e siècle, l'intérêt de l'analysis situs n'est pas passé inaperçu. En revanche, la nécessité d'un théorème équivalent à celui de l'article n'est pas encore évidente. Piers Bohl, un mathématicien live, applique des méthodes topologiques pour étudier des équations différentielles. Il démontre en 1904 le résultat de l'article pour la dimension trois ; son texte passe inaperçu^[18].

C'est finalement Brouwer, qui donne à ce théorème ses premières lettres de noblesse. Ses objectifs sont différents de ceux de Poincaré. Ce mathématicien est passionné par les fondements des mathématiques, essentiellement la logique et la topologie. Son intérêt initial réside dans une tentative de résolution du cinquième problème de Hilbert^[19]. En 1909, lors d'un voyage à Paris, il rencontre Poincaré, Hadamard et Borel. Les discussions qui s'ensuivent convainquent Brouwer de l'importance de mieux comprendre la topologie des espaces euclidiens et est l'origine d'une fructueuse relation épistolaire avec Hadamard. Durant les quatre années à venir, il se concentre pour établir certains grands théorèmes sur cette question. Cette année-là, Brouwer démontre le théorème de la boule chevelue pour la sphère de dimension deux, ainsi que le fait que toute application continue de la boule de dimension deux dans elle-même possède un point fixe^[20]. Ces deux résultats en eux-mêmes ne sont pas véritablement des nouveautés. Comme lui fait remarquer Hadamard, un équivalent du théorème de la boule chevelue est déjà démontré par Poincaré^[21]. L'aspect révolutionnaire de l'approche de Brouwer consiste en l'usage systématique d'outils développés récemment comme l'homotopie, le concept de base du groupe de Poincaré. L'année suivante, Hadamard généralise le théorème de l'article à toute dimension finie, mais à l'aide de méthodes différentes. Hans Freudenthal commente ainsi les rôles respectifs : « Comparées aux méthodes révolutionnaires de Brouwer, celles d'Hadamard sont très traditionnelles, mais la participation d'Hadamard à la naissance des idées de Brouwer ressemble plus à celle d'une sage-femme qu'à celle d'un simple spectateur »^[22].

L'approche de Brouwer porte ses fruits ; en 1912, il trouve aussi une démonstration valable pour toute dimension finie^[23], ainsi que d'autres théorèmes clé comme l'invariance de la dimension. Dans le contexte de ces travaux, Brouwer généralise aussi le théorème de Jordan à une dimension quelconque et établit les propriétés associées au degré d'une application^[19]. Cette branche des mathématiques, initialement imaginée par Poincaré et développée par Brouwer, change de nom. Dans les années 1930, l'analysis situs devient la topologie algébrique^[24].

La célébrité de Brouwer n'est pas uniquement la conséquence de ses travaux en topologie. Il est aussi auteur et ardent défenseur d'une manière de formaliser les mathématiques, appelée intuitionnisme, qui, à l'époque se voulait opposée au formalisme de la théorie des ensembles^{[Note 6]}. Si Brouwer préfère des preuves fondées sur une démonstration constructive, paradoxalement, celles qui sont à l'origine de ses grands théorèmes de topologie ne le sont pas^[25] (l'algorithme publié par Herbert Scarf en 1967, basé sur le lemme de Sperner, ne fournit qu'un « point fixe approché »^[15]).

Postérité du théorème

Le théorème du point fixe de Brouwer s'avère fondamental, au moins à deux titres. Le XX^e siècle développe de nombreux théorèmes de point fixe, et même une théorie sur cette question^[26]. Celui de Brouwer est probablement le plus important^[27]. Il est aussi l'un des théorèmes fondateurs de la topologie des variétés topologiques et est souvent utilisé pour la démonstration des autres résultats importants, comme le théorème de Jordan^[28].

Par delà les théorèmes de point fixe exploitant le caractère contractant d'une fonction, ceux directement ou indirectement issus de celui de Brouwer sont nombreux. Il n'existe pas d'application continue d'une boule fermée d'un espace euclidien dans sa frontière, laissant invariante sa frontière. Dans le même ordre d'idées, le théorème de Borsuk-Ulam indique qu'une application continue de la sphère de dimension n dans Rⁿ possède au moins deux points antipodaux de même image. Dans le cas de la dimension finie, le théorème du point fixe de Lefschetz établit en 1926^[29] une méthode pour compter les points fixes. Le théorème du point fixe de Brouwer est généralisé en 1930 aux espaces de Banach^[30]. Cette généralisation porte le nom de théorème du point fixe de Schauder, résultat encore généralisé par Shizuo Kakutani aux fonctions multivoques. On ne rencontre pas uniquement le théorème ou ses avatars en topologie. Le théorème de Hartman-Grobman, qui établit la nature qualitative du comportement de certaines équations différentielles au voisinages de certains points d'équilibre, se démontre avec le théorème du point fixe de Brouwer. Sur le même sujet, le théorème de la variété centrale (en) utilise aussi ce théorème de Brouwer pour sa démonstration. On trouve encore le théorème pour démontrer des existences de solutions à certaines équations aux dérivées partielles^[31].

D'autres domaines sont touchés. En théorie des jeux, le théorème de John Nash sur le jeu de Hex (dont la démonstration est astucieuse mais élémentaire) est en fait équivalent à celui de Brouwer^[32]. En économie, P. Bich précise que certaines généralisations du théorème montrent que son usage est utile pour « quelques problèmes classiques en théorie des jeux ou en équilibre général (modèle d’Hotelling, équilibres financiers en marchés incomplets, ...) »^[33].

Démonstrations

Préambule

Les méthodes de démonstrations sont nombreuses. L'une particulièrement simple est l'œuvre de David Gale^[32]. Elle provient d'une analyse différente des résultats de Nash sur le jeu de Hex. La preuve présentée ici s'applique à la dimension 2, mais l'article original ne contient pas cette limitation.

La topologie combinatoire est une autre méthode permettant de démontrer le théorème. Pendant les années 1920, les mathématiciens ont commencé à dégager des principes combinatoires liés au théorème de Brouwer (lemme de Sperner, lemme de Knaster-Kuratowski-Mazurkiewicz). Ces travaux offrirent à la fois de nouvelles démonstrations élégantes^[34] de ce théorème et l'amorce d'une théorie en combinatoire pour l'avenir.

D'autres utilisent la géométrie différentielle. Milnor établit un lemme qui simplifie la preuve pour les fonctions infiniment différentiables. Il devient aisé de conclure pour les fonctions continues à l'aide du théorème de Stone-Weierstrass^{[réf. nécessaire]}. L'usage de théorèmes puissants rend la démonstration plus facile. En géométrie différentielle, le théorème de Stokes implique directement celui du point fixe de Brouwer^[35], pour les fonctions de classe C². Une autre méthode consiste à faire appel à des théorèmes plus forts, comme celui de la boule chevelue^[36] ou de Borsuk-Ulam^[37].

Néanmoins, pour Daniel Leborgne^[38], les théorèmes comme celui du point fixe de Brouwer « sont habituellement démontrés par des méthodes universelles de topologie algébrique, donc, évidemment préférables ». En dimension 2, une preuve présentée ici utilise le groupe de Poincaré, qui se fonde sur la notion d'homotopie. Pour une dimension quelconque, la preuve se généralise ; la notion clé n'est plus l'homotopie mais l'homologie^[39].

Par le jeu de Hex

En 1949, Nash réinvente le jeu de Hex et montre que la partie nulle y est impossible^[40]. Sa démonstration est équivalente au théorème de l'article. Une trentaine d'années plus tard, D. Gale s'en rend compte et montre que le jeu peut servir de démonstration élémentaire au résultat de Brouwer.

Le jeu a lieu sur un plateau composé d'hexagones. À la fin du jeu, certains hexagones sont recouverts par des jetons (rouges ou bleus sur la figure de gauche). Le camp des bleus est formé par les deux côtés du plateau signalés par une ligne bleue, les deux autres côtés (signalés par une ligne rouge) constituent le camp adverse. S'il est possible de tracer une ligne blanche qui ne quitte jamais la zone des hexagones bleus et qui relie les deux côtés bleus, les bleus ont gagné, comme illustré sur la figure de gauche. De même, s'il est possible de tracer une ligne blanche qui ne quitte jamais la zone des hexagones rouges et qui relie les deux côtés rouges, les rouges ont gagné. L'article Hex montre que si le plateau est rempli de jetons, le match nul est impossible, c'est-à-dire que, soit les hexagones rouges, soit les bleus, sont support d'une ligne blanche reliant les deux côtés d'un même camp. Cette propriété permet de démontrer le théorème de Brouwer.

Trouver un point fixe d'une fonction f de K dans K revient à trouver un zéro de la fonction g, de K dans Rⁿ, qui à x associe f(x) – x. L'existence d'un tel zéro se prouve à l'aide du lemme suivant :

Démonstration du lemme dans le cas n = 2^[41]

Soit f continue de K dans K. La fonction g associée est alors continue du compact K dans R², donc uniformément continue. Il existe donc un réel strictement positif δ tel que :

${\displaystyle (1)\quad \forall x,y\in K\quad \|x-y\|<\delta \Rightarrow \|g(x)-g(y)\|<{\frac {\varepsilon }{2}}.}$

Comme expliqué au § « Dimension deux » ci-dessus, on peut supposer que la norme ║∙║ choisie sur R² est la plus grande valeur absolue des coordonnées et que le compact convexe K est la boule unité [–1, 1]×[–1, 1] pour cette norme.

Ce compact K, dont la frontière est illustrée en vert sur la figure de droite, est rempli par un plateau de hex redressé (cf l'image de droite). Le plateau contient suffisamment d'hexagones pour que chacun puisse être contenu dans un disque de diamètre δ. On note g₁ et f₁ (resp. g₂ et f₂) la première (resp. la deuxième) coordonnée des fonctions g et f. En faisant jouer au hex, les fonctions g₁ et g₂, on démontre le lemme.

Soit B_f l'ensemble des hexagones tels que g₁ soit strictement supérieure à ε/2 sur l'intégralité de l'hexagone. Ces hexagones sont dessinés en bleu foncé sur la figure. On considère les hexagones recouvrant la zone {1}×[–1, 1] et x un élément de cette zone. La fonction g₁ au point x vaut f₁(x) – 1 c'est-à-dire un nombre nécessairement négatif. Ceci montre qu'aucun hexagone contenant un point de {1}×[–1, 1] ne peut être bleu foncé. Soit B_c l'ensemble des hexagones tel que g₁ soit strictement inférieure à –ε/2 sur l'intégralité de l'hexagone. Ces hexagones sont dessinées en bleu clair sur la figure. Le raisonnement précédent montre que la zone {–1}×[–1, 1] ne peut contenir aucun hexagone bleu clair.

Cet argument montre que si les hexagones bleus, clairs ou foncés, représentent les pions d'un joueur, ce joueur ne peut avoir gagné. L'argument précédent montre qu'il n'existe aucune possibilité d'une suite connexe d'hexagones bleus uniquement clairs ou uniquement foncés reliant les deux bords. Or deux hexagones bleus, l'un clair et l'autre foncé, ne peuvent être connexes. Ils partageraient une arête sur laquelle la fonction g₁ serait à la fois strictement positive et strictement négative.

On définit de même R_f (resp. R_c) l'ensemble des hexagones qui ne sont pas bleus et tels g₂ soit strictement supérieur à ε/2 (resp. inférieur à –ε/2) sur tout l'hexagone. Le même raisonnement précédent montre que les hexagones rouges (union des R_f rouge foncé et R_c rouge clair) ne représentent pas non plus une configuration gagnante.

Le résultat, montré dans l'article hex, permet de déduire qu'il existe un hexagone qui n'est ni rouge ni bleu. Par définition, un tel hexagone contient un point x dont l'image par g₁ est, en valeur absolue plus petite que ε/2, et un point y dont l'image par g₂ est, en valeur absolue aussi plus petite que ε/2. Comme x et y sont situés à une distance plus petite que δ l'un de l'autre, les normes de g(x) et de g(y) sont plus petites que ε, d'après la majoration (1).

Ce lemme prouve que la borne inférieure sur K de la fonction ║g║ est nulle. Puisque cette fonction est continue et que K est compact, cette borne est atteinte, c'est-à-dire qu'il existe un point m de K tel que ║g(m)║ = 0, autrement dit tel que g(m) = 0, ce qui démontre le théorème.

Par une méthode homotopique

Comme annoncé en préambule de cette section, la preuve présentée ici est spécifique à la dimension 2.

Ici, il est plus simple d'identifier le cercle avec les points du plan complexe de module 1 et le disque avec les points de modules inférieurs ou égaux à 1. Il existe une différence topologique entre le disque et le cercle. Soit un point A du disque et un lacet d'extrémités A, c'est-à-dire un chemin continu qui part de A, sans jamais quitter le disque, pour retourner au point A. Si le lacet est matérialisé par un fil élastique, on peut tirer sur chacune des extrémités du chemin pour finir par un chemin composé d'un point unique : A. Autrement dit, on peut déformer continument le lacet jusqu'à n'obtenir qu'un point. Cette propriété est illustrée sur la figure de gauche, le lacet bleu est continument déformé pour obtenir un chemin de plus en plus proche du lacet constant égal à A. On dit que tout lacet est homotope à un point. Sur le cercle, cette propriété n'est pas vraie. On peut imaginer un chemin qui part du point B, fait le tour du cercle et revient en B. On obtient un lacet d'extrémités B et qui parcourt le cercle. Cette fois-ci, on aura beau tirer sur le chemin ou le fil élastique, qui ne peut par définition pas quitter le cercle, il n'y aura pas moyen de le ramener au point B sans le rompre. En termes mathématiques, on dit que le groupe fondamental du disque est trivial, alors que celui du cercle ne l'est pas.

Si une exception au théorème de Brouwer existait, il serait possible de créer un lacet qui ferait le tour du cercle en allant toujours dans la même direction, et qui serait pourtant homotope à un point. Cette impossibilité est la clé de la démonstration proposée ici. Dans un premier temps, on démontre la propriété suivante :

• Il n'existe pas de fonction continue du disque dans le cercle, qui laisse invariant chaque point du cercle.

Ce qui se dit encore : il n'existe pas de rétraction forte par déformation du disque sur sa frontière. En effet, s'il y en avait une que l'on note F, on définirait la fonction H par :

${\displaystyle \forall t,x\in [0,1],\quad H(t,x)=F{\big (}xe^{2{\rm {i}}\pi t}{\big )}.}$

Si x est égal à 1, on obtient un lacet d'extrémités le point 1 et qui fait le tour du disque, si t varie. Si x est égal à 0, on obtient un lacet constant de valeur F(0). Le lacet initial serait homotope à un point, comme cette propriété est fausse dans le cercle, la proposition est démontrée. L'article détaillé propose une démarche plus rapide, elle suppose néanmoins l'acquisition de concepts plus lourds à mettre en œuvre.

Il reste encore à construire la fonction F.

• S'il existe une fonction continue du disque dans lui-même sans point fixe, il existe une rétraction forte par déformation du disque sur sa frontière^[42].

On considère le segment passant par x et f(x) et d'extrémités f(x) et un point du cercle. Cette construction est illustrée sur la figure de droite. Comme x et f(x) ne sont jamais confondus, la fonction F est parfaitement définie. Si x est sur la frontière, les points x et F(x) sont confondus. Il est relativement simple de montrer que F est continue.

Détails de la démonstration

Le lacet α est celui qui à t, élément de [0, 1], associe exp(2πit). Il n'est pas homotope au lacet c constant toujours égal à 1. Cette vérité est en général démontrée dans un résultat plus large, établissant la structure du groupe fondamental du cercle^{[Note 7]}. On peut néanmoins procéder plus directement. Intuitivement, si le lacet s'imagine comme un fil qui tourne autour du cercle, tirer suffisamment fort sur les deux brins que l'on trouve au point 1 pour ramener l'intégralité du fil en 1, va casser le fil. Trouver le point de cassure est une méthode pour exhiber une discontinuité^{[Note 8]}. Cette propriété permet d'établir le résultat suivant.

• Il n'existe pas de rétraction forte par déformation du disque dans le cercle :

On raisonne par l'absurde et l'on suppose qu'il existe une telle rétraction F. On considère la fonction H(t, x) de [0, 1]² dans le cercle, définie par :

${\displaystyle \forall t,x\in [0,1]\quad H(t,x)=F{\big (}x\exp(2\pi {\rm {i}}t){\big )}.}$

Si x est égal à 1, comme la rétraction est la fonction identité sur le cercle, le lacet qui à t associe H(t, 1) est bien égal à α. Si x est égal à 0, la fonction qui à t associe H(t, 0) est constante. Comme la fonction H est continue, on aurait montré que le lacet α est homotope à un point. La rétraction ne peut donc exister, d'après la première proposition.

• Si une fonction f du disque dans lui-même est sans point fixe et continue, il existe une rétraction forte par déformation, F, du disque dans le cercle :

La fonction F est définie comme indiqué précédemment. Il faut encore montrer qu'elle est continue. On cherche le point appartenant au cercle unité et à la demi-droite d'origine x et dirigée par le vecteur x – f(x). Ce point est l'image d'une valeur positive (ou nulle) de t par la fonction qui, à t, associe x + t(x – f(x)). Plus exactement, t est l'unique racine positive du polynôme P(t), défini par (║∙║ désigne la norme euclidienne) :

${\displaystyle P(t)=\|x+t{\big (}x-f(x){\big )}\|^{2}-1.}$

Ce polynôme est du second degré et s'écrit encore a(x)t² + b(x)t + c(x), ici a(x), b(x) et c(x) désignent trois fonctions continues définies sur le disque et à valeurs dans R. On remarque que le coefficient du monôme dominant a(x) est toujours strictement positif (car x est différent de f(x) d'après les hypothèses retenues) et les images du polynôme en 0 et en –1 sont négatives. Un tel polynôme admet toujours une unique racine positive et elle s'écrit comme une fonction, notée λ, continue des trois coefficients a(x), b(x) et c(x). On en déduit que λ est une fonction continue de x et la rétraction F(x), qui s'écrit :

${\displaystyle \displaystyle F(x)=x+\lambda (x){\big (}x-f(x){\big )},}$

est aussi continue.

Par la formule de Stokes

Pour montrer qu'une application a au moins un point fixe, on peut supposer qu'elle est lisse. En effet, si une application qui n'a pas de point fixe est convolée avec une fonction lisse ayant un support suffisamment petit, alors la fonction lisse obtenue est aussi sans point fixe.

On note B et S la boule unité fermée et la sphère unité d'un espace euclidien. Soit ${\displaystyle f:B\to B}$ une application lisse sans point fixe. Soit, comme plus haut, ${\displaystyle F:B\to S}$ définie par : ${\displaystyle F(x)\in S}$ et ${\displaystyle x\in [f(x),F(x)]}$. Comme f n'a pas de point fixe, F est bien définie et lisse, et c'est une rétraction de B sur S : ${\displaystyle F\circ i=\mathrm {Id} _{S}}$, où ${\displaystyle i:S\to B}$ est l'inclusion.

Soit ${\displaystyle \omega }$ la forme volume (fermée) de la sphère S. Alors :

${\displaystyle {\begin{aligned}0<\int _{S}\omega &=\int _{S}i^{*}(F^{*}(\omega ))&{\text{(}}F\circ i=\mathrm {Id} _{S}{\text{)}}\\&=\int _{B}dF^{*}(\omega )&{\text{ (Formule de Stokes)}}\\&=\int _{B}F^{*}(d\omega )&{\text{ (Propriété du tiré en arrière) }}\\&=\int _{B}F^{*}(0)=0&{\text{(}}\omega {\text{ est fermée),}}\end{aligned}}}$

ce qui est absurde. On en déduit que f admet au moins un point fixe.

La même démonstration prouve également qu'il n'y a pas de rétraction lisse d'une variété lisse orientable compacte sur son bord.

Par le théorème de la boule chevelue

Le théorème de la boule chevelue énonce que sur une sphère unité de dimension paire (c'est-à-dire la sphère de rayon 1 et de centre le vecteur nul, dans un espace euclidien de dimension impaire), il n'existe pas de champ de vecteurs α qui soit continu, tangent à la sphère en tout point x de cette sphère (c'est-à-dire vérifiant (x|α(x)) = 0), et qui ne s'annule jamais. On l'exprime parfois en disant qu'il existe toujours un point de la Terre où le vent est inexistant.

S'il existe une fonction f de la boule unité fermée Bⁿ sans point fixe, on construit deux champs de vecteurs, sur la sphère unité de dimension n et celle de dimension n +1, dont l'un des deux contredit le théorème de la boule chevelue. L'avantage de cette méthode est qu'elle n'utilise que des techniques élémentaires, sa faiblesse réside dans une démarche moins universelle que celle de la topologie algébrique, qui permet de démontrer des résultats plus forts, comme le théorème de Borsuk-Ulam.

Détails de la démonstration

Notons S^n–1 la sphère unité de Rⁿ (c'est la frontière de Bⁿ). La démonstration est par l'absurde et en trois étapes :

1. s'il existe une application continue f sans point fixe de Bⁿ dans elle-même, il en existe aussi une g de Bⁿ⁺¹ dans elle-même ;
2. s'il existe une application continue sans point fixe de B^m dans elle-même, il existe sur la sphère S^m un champ α de vecteurs non nuls tel que (x|α(x)) = 0 pour tout x de cette sphère ;
3. en appliquant la deuxième étape à f, et au g déduit de f par la première étape, on obtient deux champs de vecteurs (l'un sur Sⁿ, l'autre sur Sⁿ⁺¹), qui d'après le théorème de la boule chevelue prouvent que n n'est ni pair, ni impair, d'où la contradiction souhaitée.

Il reste à détailler les deux premières étapes.

• Etape 1.

En utilisant que B^m est homéomorphe à [–1, 1]^m (pour m = n et pour m = n + 1), on se ramène à démontrer que s'il existe une application continue F sans point fixe de [–1, 1]ⁿ dans lui-même, il en existe aussi une G de [–1, 1]ⁿ⁺¹ dans lui-même.

L'assertion devient ainsi immédiate : il suffit de poser G(x, t) = (F(x), t), pour tout x de [–1, 1]ⁿ et tout t de [–1, 1].

• Etape 2.

Soit h une application continue sans point fixe de B^m dans elle-même. Posons

${\displaystyle \forall x\in B^{m}\quad H(x)=(1-(x|h(x)))x-(1-\|x\|^{2})h(x).}$

Du fait que h est sans point fixe on déduit que pour x intérieur à la boule, H(x) est non nul, et que pour x sur la sphère on a même (x|H(x)) = 1 – (x|h(x)) > 0.

Posons ensuite, en désignant par x les m premières coordonnées d'un vecteur X de R^m+1 et par t sa dernière coordonnée :

${\displaystyle \forall X=(x,t)\in S^{m}\quad \alpha (X)=(-tH(x),(x|H(x))).}$

Manifestement, la fonction α est continue et vérifie (X|α(X)) = 0. Enfin, α(X) n'est jamais nul (car si x est de norme 1, (x|H(x)) est non nul, et si x est de norme strictement inférieure à 1, t et H(x) sont non nuls).

Par le lemme de Sperner

Au lieu de montrer le théorème pour la boule ${\displaystyle B}$ de dimension ${\displaystyle d}$, on le montre pour le simplexe ${\displaystyle T_{d}=\{(x_{1},\ldots ,x_{d+1})\in \mathbb {[} 0,1]^{d+1}|\sum _{k=1}^{d+1}x_{k}=1\}}$ qui lui est homéomorphe.

Soit ${\displaystyle f:T_{d}\to T_{d}}$ une fonction continue.

Si ${\displaystyle v\in T_{d}}$ n'est pas un point fixe, on définit sa couleur ${\displaystyle C(v)=\min\{i|(f(v_{i}))_{i}<v_{i}\}}$, de sorte que ${\displaystyle (f(v))_{C(v)}<v_{C(v)}}$ (${\displaystyle \{i|(f(v_{i}))_{i}<v_{i}\}}$ est non vide, sinon on aurait ${\displaystyle (f(v))_{i}-v_{i}\geq 0,\sum _{i=1}^{d+1}(f(v))_{i}-v_{i}=0}$ et donc ${\displaystyle v-f(v)=0}$).

Soit ${\displaystyle r}$ un entier strictement positif. On subdivise ${\displaystyle T_{d}}$ en ${\displaystyle r^{d}}$ simplexes de la forme ${\displaystyle T_{d}\cap \prod _{k=1}^{d+1}[{\frac {\alpha _{k}}{r}},{\frac {\alpha _{k}+1}{r}}]}$ pour ${\displaystyle \alpha _{k}\in \mathbb {N} }$ tels que ${\displaystyle \sum _{k=1}^{d+1}\alpha _{k}=r-1}$.

Si l'un des points ${\displaystyle v=(v_{1},\ldots ,v_{d+1})\in T_{d}\cap ({\frac {1}{r}}\mathbb {N} )^{d+1}}$ de cette subdivision est un point fixe, l'existence du point fixe est prouvée, sinon, on colorie ${\displaystyle v}$ par ${\displaystyle C(v)}$.

Cette coloration vérfie les hypothèses du lemme de Sperner: chaque sommet de ${\displaystyle T_{d}}$ est d'une couleur différente (${\displaystyle C((\delta _{ik})_{1\leq k\leq d+1})=i}$), si un des sommets ${\displaystyle v}$ de la subdivision est dans l'enveloppe convexe de ${\displaystyle A^{1},\ldots ,A^{s}}$ sommets de ${\displaystyle T}$ alors ${\displaystyle C(v)\in \{C(A^{1}),\ldots ,C(A^{s})\}}$.

Il existe donc un simplexe de la subdivision tel que chacun de ses sommets soit de couleur différente. Soient ${\displaystyle D^{r,k}}$ les sommets de ce simplexe, ordonnés de telle sorte que ${\displaystyle C(D^{r,k})=k}$. On a de plus ${\displaystyle \|D^{r,1}-D^{r,k}\|\leq {\frac {1}{r}}}$.

Comme ${\displaystyle T_{d}}$ est compact, ${\displaystyle (D^{n,1})_{n\in \mathbb {N} }}$ admet une sous-suite convergente ${\displaystyle (D^{\phi (n),1})_{n\in \mathbb {N} }}$, vers une limite ${\displaystyle x}$. C'est aussi la limite de ${\displaystyle (D^{\phi (n),k})_{n\in \mathbb {N} }}$ pour ${\displaystyle k\in \{1,\ldots ,d+1\}}$.

Comme ${\displaystyle (D^{\phi (n),k})_{k}>(f(D^{\phi (n),k}))_{k}}$, on en déduit par passage à la limite ${\displaystyle x_{k}\geq (f(x))_{k}}$. Comme ${\displaystyle \sum _{k=1}^{d+1}x_{k}-(f(x))_{k}=0}$, on en déduit ${\displaystyle f(x)-x=0}$, ce qui prouve l'existence du point fixe.

Liens externes

• A. Monier, « Le théorème de Brouwer », École normale supérieure de Lyon, Le journal de maths des élèves, vol. 1, n^o  4, 1998, p. 202-206
• Jean Mawhin, Autour du théorème du point fixe, 2004

Notes et références

Notes

Références

• (en) H. Freudenthal, « The cradle of modern topology, according to Brouwer's inedita », Hist. Math., vol. 2,‎ 1975, p. 495-502
• (en) Vasile I. Istratescu, Fixed Point Theory : An Introduction, Kluwer Academic Publishers, 2001, 488 p. (ISBN 978-1-4020-0301-1, OCLC 171109810, lire en ligne)
  Ce livre parcourt de nombreux théorèmes de point fixe. Le chapitre III est consacré à ceux issus d'une application contractante. Le chapitre IV traite le théorème de Brouwer. La démarche proposée pour la preuve utilise la géométrie différentielle élémentaire.
• D. Leborgne, Calcul différentiel et géométrie, Paris, Puf, 1982 (ISBN 978-2-13-037495-4)
  Ce livre présente une démonstration du théorème de l'article issue de la géométrie différentielle. Elle fait usage du lemme de Milnor.
• D. Violette, « Applications du lemme de Sperner pour les triangles », Bulletin AMQ, vol. XLVI, n^o 4,‎ 2006 (lire en ligne)

• Portail des mathématiques