Se ha sugerido que esta página sea renombrada como «Distribución Gamma ». Motivo : Cambio a común en español (ver discusión)
Función de Densidad de una Gama. En teoría de probabilidad y Estadística, la distribución gamma es una distribución con dos parámetros que pertenece a las distribuciones de probabilidad continuas. La distribución exponencial , distribución de Erlang y la distribución χ² son casos particulares de la distribución gamma. Hay dos diferentes parametrizaciones que suelen usarse
Con parámetro de forma k {\displaystyle k} θ {\displaystyle \theta } Con parámetro de forma α = k {\displaystyle \alpha =k} λ = 1 / θ {\displaystyle \lambda =1/\theta } Definición Notación Si una variable aleatoria continua X {\displaystyle X} distribución gamma con parámetros α > 0 {\displaystyle \alpha >0} λ > 0 {\displaystyle \lambda >0} X ∼ Γ ( α , λ ) {\displaystyle X\sim \Gamma (\alpha ,\lambda )}
Función de Densidad Si X ∼ Γ ( α , λ ) {\displaystyle X\sim \Gamma (\alpha ,\lambda )} función de densidad es
f X ( x ) = λ Γ ( α ) ( λ x ) α − 1 e − λ x {\displaystyle f_{X}(x)={\frac {\lambda }{\Gamma (\alpha )}}(\lambda x)^{\alpha -1}e^{-\lambda x}} para x > 0 {\displaystyle x>0}
Γ ( α ) = ∫ 0 ∞ t α − 1 e − t d t {\displaystyle \Gamma (\alpha )=\int _{0}^{\infty }t^{\alpha -1}e^{-t}dt} es la función gamma y satisface
Γ ( 2 ) = Γ ( 1 ) = 1 {\displaystyle \Gamma (2)=\Gamma (1)=1} Para cualquier α > 0 {\displaystyle \alpha >0} Γ ( α + 1 ) = α Γ ( α ) {\displaystyle \Gamma (\alpha +1)=\alpha \Gamma (\alpha )} Si n ∈ Z + {\displaystyle n\in \mathbb {Z} ^{+}} Γ ( n + 1 ) = n ! {\displaystyle \Gamma (n+1)=n!} Γ ( 1 2 ) = π {\displaystyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}} Si n ∈ Z + {\displaystyle n\in \mathbb {Z} ^{+}} Γ ( n 2 ) = π ( n − 1 ) ! 2 n − 1 ( n − 1 2 ) ! {\displaystyle \Gamma \left({\frac {n}{2}}\right)={\frac {{\sqrt {\pi }}(n-1)!}{2^{n-1}\left({\frac {n-1}{2}}\right)!}}} Función de Densidad Acumulada La función de distribución acumulada de una variable aleatoria X ∼ Γ ( α , λ ) {\displaystyle X\sim \Gamma (\alpha ,\lambda )}
F X ( x ) = ∫ 0 x λ Γ ( α ) ( λ y ) α − 1 e − λ y d y {\displaystyle F_{X}(x)=\int _{0}^{x}{\frac {\lambda }{\Gamma (\alpha )}}(\lambda y)^{\alpha -1}e^{-\lambda y}\;dy} Si X {\displaystyle X} X ∼ Γ ( n , λ ) {\displaystyle X\sim \Gamma (n,\lambda )} n ∈ Z + {\displaystyle n\in \mathbb {Z} ^{+}} X {\displaystyle X} distribución de Erlang ) entonces su función de distribución acumulada está dada por
F X ( x ) = 1 − ∑ k = 0 n − 1 ( λ x ) k k ! e − λ x = ∑ k = n ∞ ( λ x ) k k ! e − λ x {\displaystyle {\begin{aligned}F_{X}(x)&=1-\sum _{k=0}^{n-1}{\frac {(\lambda x)^{k}}{k!}}e^{-\lambda x}\\&=\sum _{k=n}^{\infty }{\frac {(\lambda x)^{k}}{k!}}e^{-\lambda x}\end{aligned}}} Propiedades Si X {\displaystyle X} X ∼ Γ ( α , λ ) {\displaystyle X\sim \Gamma (\alpha ,\lambda )} X {\displaystyle X}
Media La media de la variable aleatoria X {\displaystyle X}
E [ X ] = α / λ {\displaystyle {\text{E}}[X]=\alpha /\lambda }
Varianza La varianza de la variable aleatoria X {\displaystyle X}
Var [ X ] = α λ 2 {\displaystyle {\text{Var}}[X]={\frac {\alpha }{\lambda ^{2}}}} Momentos El n {\displaystyle n} variable aleatoria X {\displaystyle X}
E [ X n ] = α ( α + 1 ) ⋯ ( α + n − 1 ) λ n {\displaystyle \operatorname {E} [X^{n}]={\frac {\alpha (\alpha +1)\cdots (\alpha +n-1)}{\lambda ^{n}}}} para n ∈ N {\displaystyle n\in \mathbb {N} }
Función generadora de momentos La función generadora de momentos está dada por
M X ( t ) = ( λ λ − t ) α {\displaystyle M_{X}(t)=\left({\frac {\lambda }{\lambda -t}}\right)^{\alpha }} para λ > t {\displaystyle \lambda >t}
Suma de Gammas Si X i ∼ Γ ( α i , λ ) {\displaystyle X_{i}\sim \Gamma (\alpha _{i},\lambda )} i = 1 , 2 , … , n {\displaystyle i=1,2,\dots ,n}
∑ i = 1 n X i ∼ Γ ( ∑ i = 1 n α i , λ ) {\displaystyle \sum _{i=1}^{n}X_{i}\sim \Gamma \left(\sum _{i=1}^{n}\alpha _{i},\lambda \right)} Escalar Si X ∼ Γ ( α , λ ) {\displaystyle X\sim \Gamma (\alpha ,\lambda )} c > 0 {\displaystyle c>0}
c X ∼ Γ ( α , λ / c ) {\displaystyle cX\sim \Gamma \left(\alpha ,\lambda /c\right)} Media Logarítmica Puede demostrarse que
E [ ln ( X ) ] = ψ ( α ) − ln ( λ ) {\displaystyle \operatorname {E} [\ln(X)]=\psi (\alpha )-\ln(\lambda )} donde ψ {\displaystyle \psi } función digamma .
Cálculo de Probabilidades en R Se puede utilizar R (lenguaje de programación) para hallar los valores de la función de densidad f ( x ) {\displaystyle f(x)} función de distribución F ( x ) {\displaystyle F(x)} variable aleatoria continua X ∼ Γ ( α , λ ) {\displaystyle X\sim \Gamma (\alpha ,\lambda )}
Función de densidad Para x > 0 {\displaystyle x>0}
f X ( x ) = λ Γ ( α ) ( λ x ) α − 1 e − λ x {\displaystyle f_{X}(x)={\frac {\lambda }{\Gamma (\alpha )}}(\lambda x)^{\alpha -1}e^{-\lambda x}} entonces para evaluar la función de densidad f X ( x ) {\displaystyle f_{X}(x)}
# d=density function
dgamma ( x , α, λ)
Función de Distribución La función de distribución acumulada de la distribución Gamma está dada por
F X ( x ) = ∫ 0 x λ Γ ( α ) ( λ y ) α − 1 e − λ y d y {\displaystyle F_{X}(x)=\int _{0}^{x}{\frac {\lambda }{\Gamma (\alpha )}}(\lambda y)^{\alpha -1}e^{-\lambda y}\;dy} para x > 0 {\displaystyle x>0} F X ( x ) {\displaystyle F_{X}(x)}
# p=probability distribution function
pgamma ( x , α, λ)
Distribuciones Relacionadas Si X 1 , X 2 , … , X n {\displaystyle X_{1},X_{2},\dots ,X_{n}} X i ∼ Exp ( λ ) {\displaystyle X_{i}\sim {\text{Exp}}(\lambda )} ∑ i = 1 n X i ∼ Γ ( n , λ ) {\displaystyle \sum \limits _{i=1}^{n}X_{i}\sim \Gamma \left(n,\lambda \right)} distribución de Erlang y es un caso particular de la distribución gama cuando el parámetro α = n ∈ N {\displaystyle \alpha =n\in \mathbb {N} } Si X ∼ Γ ( 1 , λ ) {\displaystyle X\sim \Gamma \left(1,\lambda \right)} X ∼ Exp ( λ ) {\displaystyle X\sim {\text{Exp}}(\lambda )} Si X ∼ Γ ( n 2 , 1 2 ) {\displaystyle X\sim \Gamma \left({\frac {n}{2}},{\frac {1}{2}}\right)} n ∈ N {\displaystyle n\in \mathbb {N} } X ∼ χ n 2 {\displaystyle X\sim \chi _{n}^{2}} Véase también Enlaces externos Q117806 Gamma distribution / Q117806 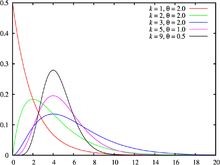
 Datos: Q117806
Datos: Q117806 Multimedia: Gamma distribution / Q117806
Multimedia: Gamma distribution / Q117806






























![{\displaystyle {\text{E}}[X]=\alpha /\lambda }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e9d09169f4d133d994eaa85c554dac08a191b4b)
![{\displaystyle {\text{Var}}[X]={\frac {\alpha }{\lambda ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e324c06c297528e5d3a63f9176abcf9f13a6d3a8)

![{\displaystyle \operatorname {E} [X^{n}]={\frac {\alpha (\alpha +1)\cdots (\alpha +n-1)}{\lambda ^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d94f00117e39d9131ca916aaf8a81b019db436be)








![{\displaystyle \operatorname {E} [\ln(X)]=\psi (\alpha )-\ln(\lambda )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/851a0a36812edea4802f79b097400b31e049ad46)























