Kongruenzgenerator
Die Kongruenzgeneratoren bilden eine Klasse von Algorithmen, die zufällig aussehende Zahlenfolgen erzeugen. Die dadurch erzeugten Zahlen nennt man Pseudozufallszahlen, da sie deterministisch erzeugt werden und somit nicht wirklich zufällig sind. Kongruenzgeneratoren sind die bekanntesten und meistverwendeten rekursiven arithmetischen Zufallszahlengeneratoren.
Allgemeiner Kongruenzgenerator
Ein Kongruenzgenerator wird durch folgende Parameter definiert:
- Anzahl der Zustandswerte
- Modul
- Faktoren mit
- Inkrement
- Startwerte (nicht alle 0, wenn )
Für setzt man nun
- . Dabei bezeichnet den Divisionsrest; siehe Modulo.
Die so berechneten werden als Zufallszahlen verwendet.
Der Zustand des Generators vor der Erzeugung von wird durch die Werte gegeben. Dieser Zustand legt (bei gegebenen ) alle folgenden Zufallszahlen fest, da die nächste Zufallszahl und der nächste Zustand durch den aktuellen Zustand determiniert werden. Es gibt mögliche Zustände, und deshalb muss spätestens nach Schritten ein früherer Zustand wiederholt werden. Der Kongruenzgenerator erzeugt somit eine periodische Folge von Zahlen, wobei die Periodenlänge auch wesentlich kleiner als sein kann. Im Extremfall ist sie 1, und der Generator erzeugt immer die gleiche „Zufallszahl“. Bei der Festlegung der Parameter kommt es somit unter anderem darauf an, eine ausreichende Periodenlänge sicherzustellen.
Braucht man reelle Zufallszahlen im Intervall , so kann man dafür die Näherung
verwenden, falls der Modulo groß genug ist, um eine ausreichend feine Unterteilung zu ergeben.
Linearer Kongruenzgenerator
Mit erhält man den Sonderfall eines linearen Kongruenzgenerators. Bei wird er als multiplikativer Kongruenzgenerator bezeichnet, und für andere als gemischter linearer Kongruenzgenerator.
Letzterer wird häufiger verwendet und hat vier natürliche Zahlen als Parameter:
- Modul
- Faktor
- Inkrement
- Startwert
Aus dem Startwert werden dann die weiteren Werte nach folgender Formel (mit ) berechnet:
Der lineare Kongruenzgenerator wurde 1949 von Derrick Henry Lehmer eingeführt.[1] Er wird in den Laufzeitbibliotheken verschiedener Programmiersprachen zur Erzeugung von Pseudozufallszahlen verwendet, z. B. in C/C++ in der Funktion rand() in der Headerdatei stdlib.h.[2]
In der Kryptographie dagegen kommt der lineare Kongruenzgenerator nicht zum Einsatz, da man schon aus wenigen Werten der erzeugten Zahlenfolge die Parameter und und damit die vollständige Zahlenfolge berechnen kann.
Periodenlänge
Lineare Kongruenzgeneratoren erreichen nach dem Satz von Knuth genau dann ihre maximal mögliche Periodenlänge , wenn die folgenden Voraussetzungen erfüllt sind:
- Das Inkrement ist zum Modul teilerfremd.
- Jeder Primfaktor von teilt .
- Wenn durch 4 teilbar ist, dann auch .
In diesem Fall erzeugt der Generator jede Zahl von 0 bis genau einmal und beginnt dann wieder von vorn. Er liefert also eine pseudozufällige Permutation dieser Zahlen. Der Startwert kann dann jede Zahl aus dieser Menge sein.
Der multiplikative Kongruenzgenerator (mit ) muss somit eine Periodenlänge kleiner als haben. Der Satz von Carmichael besagt: bei gegebenem ist seine Periodenlänge genau dann maximal, wenn gilt:
- ist zu teilerfremd,
- ist ein primitives Element modulo .
Für einige Sonderfälle von können die primitiven Elemente modulo leicht bestimmt werden:
- Ist eine Zweierpotenz , dann muss mod 8 den Rest 3 oder 5 liefern. Die Periodenlänge ist dann , und der Startwert muss ungerade sein. Es gibt zwei Perioden, die jeweils die Hälfte der ungeraden Zahlen von bis umfassen.
- Wenn eine Primzahl ist, dann muss für alle Primfaktoren von gelten:
. Dann beträgt die Periodenlänge . Der Startwert darf nicht Null sein.
Mängel der erzeugten Zahlen
Der lineare Kongruenzgenerator liefert keine vollkommen zufällig erscheinenden Zahlen. Man kann nachweisen, dass eine Abhängigkeit von aufeinanderfolgenden Zahlen besteht.
Teilperiode
Oft wählt man , wobei die Wortlänge des Rechners in Bit ist, denn dann muss man die Modulo-Division nicht explizit berechnen. Sie ergibt sich von selbst durch das Abschneiden der Überlauf-Bits. In diesem Fall verhalten sich die niederwertigsten Bits der Zustandszahl wie ein Generator mit dem Modul . Diese Bits wiederholen sich also spätestens nach Schritten. Dies bedeutet insbesondere, dass das niederwertigste Bit bestenfalls die Periode 2 besitzt, also regelmäßig zwischen 0 und 1 wechselt. Beim multiplikativen Kongruenzgenerator ist es sogar konstant.
Allgemein gilt für alle linearen Kongruenzgeneratoren: wenn ein Teiler des Moduls ist, dann ergibt eine Zahlenfolge mit der Periode :
- für ein gilt: .
Wenn der Generator nach dem Satz von Knuth die Periode hat, dann beträgt die Länge der Teilperiode genau für alle Teiler von .
Wegen dieses Teilperioden-Verhaltens ist es ungünstig, Zufallszahlen durch zu gewinnen, wenn und nicht teilerfremd sind. Dann würde der Divisionsrest für eine Zahl , die und teilt, eine Periode der Länge höchstens durchlaufen. Wenn man z. B. einen sechsseitigen Würfel simulieren will und gerade ist, dann liefert Zahlen, die abwechselnd gerade und ungerade sind.
Mögliche Abhilfe:
- Man nutzt einen gemischten linearen Kongruenzgenerator mit Periode , wobei man den Modul zu teilerfremd wählt. Die Ergebnisse sind nicht gleichverteilt, aber bei ist die Abweichung von der Gleichverteilung nur gering und kann oft vernachlässigt werden.
- Man nutzt einen multiplikativen Kongruenzgenerator mit Periode und wählt für eine große Primzahl. Wenn außerdem ein Vielfaches von ist, sind die auch gleichverteilt.
- Man setzt und wendet mit den höchstwertigen Bits von eine Verwerfungsmethode an. Die werden um Bit nach rechts geschoben, wobei die kleinste Zweierpotenz ist: . Dabei verwendet man nur die , die übrigen werden verworfen. Diese Methode liefert gleichverteilte Ergebnisse.
- Man berechnet , wobei die kleinste zu teilerfremde Zahl ist, und werden verworfen.
- Manche Implementierungen eines linearen Kongruenzgenerators umgehen das Problem, indem sie nur den höherwertigen Teil des Zustandswertes als Ergebnis liefern. Z. B. ist und das dem Nutzer gelieferte Ergebnis ist mit .
Hyperebenen-Verhalten
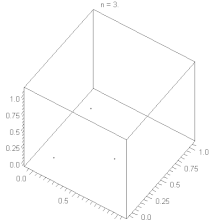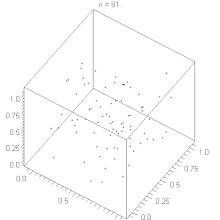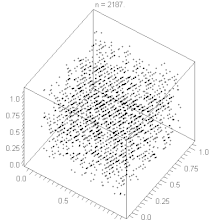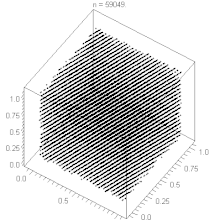

Der lineare Kongruenzgenerator weist ein Hyperebenen-Verhalten auf, siehe Satz von Marsaglia. Durch geeignete Wahl der Parameter , und kann man das Verhalten des Generators optimieren und eine große Zahl von Hyperebenen erreichen. Bei gegebenem kann man nach folgenden Faustregeln bilden:
- sollte weder zu groß noch zu klein sein, etwa:
- sollte möglichst zufällig gewählt werden, also nicht in dualer oder dezimaler Darstellung eine „runde“ Zahl sein.
- Beim gemischten linearen Kongruenzgenerator sollte die Potency möglichst groß sein. Sie ist der minimale Wert , für den ein Vielfaches von ist. Donald E. Knuth empfiehlt, dass die Potency mindestens 5 sein sollte. Wenn , dann sollte sein, um die maximal mögliche Potency zu erhalten.
Wenn man sichergehen will, dass der Generator gute Zufallszahlen erzeugt, sollte man sich nicht allein auf diese Faustregeln verlassen, sondern den Generator mit dem Spektraltest prüfen.
Wegen des Hyperebenen-Verhaltens greift man statt auf den linearen Kongruenzgenerator gelegentlich auf den inversen Kongruenzgenerator zurück, der dieses Problem nicht aufweist. Allerdings erfordert er einen höheren Rechenaufwand. Er ist kein Spezialfall des allgemeinen Kongruenzgenerators.
Programmierung
Das folgende Programm in der Programmiersprache C++ implementiert einen linearen Kongruenzgenerator mit , und , der nur die 32 höchstwertigen Bits jeder erzeugten Zufallszahl ausgibt und die niederwertigen, die von geringerer Qualität sind, verwirft. Das Programm erzeugt 10 Zufallszahlen, die in einem Array gespeichert und anschließend auf der Konsole ausgegeben werden.[3][4]
#include <iostream> #include <stdint.h> using std::cout; using std::endl; // Funktion, die die Zufallszahlen erzeugt void linearCongruentialGenerator(uint64_t &y, uint32_t *randNumbers, int count) { const uint64_t a = 6364136223846793005; const uint64_t b = 2531011; uint64_t r = y; // lokale Variable für die Berechnung for (int i = 0; i < count; i++) { r = a * r + b; randNumbers[i] = r >> 32; } y = r; // Zustand zurückschreiben } int main() { const int count = 10; // Anzahl der Zufallszahlen uint32_t randNumbers[count]; // Array für die Zufallszahlen const uint64_t seed = 12345; // Startwert für den Generator uint64_t y = seed; // Zustand des Generators linearCongruentialGenerator(y, randNumbers, count); // Erzeugung der Zufallszahlen for (int i = 0; i < count; i++) { cout << randNumbers[i] << endl; // Ausgabe auf der Konsole } }
Fibonacci-Generator
Ein Fibonacci-Generator ist ebenfalls ein Kongruenzgenerator (mit , und ) und besteht aus folgenden Komponenten:
- Modul
- Startwerte
Es sollte sein.
Mit folgender Bildungsregel werden die Pseudozufallszahlen erzeugt:
Eine Eigenschaft ist, dass die Fälle bzw. nie auftreten. Fibonacci-Generatoren sind daher als Pseudozufallszahlengeneratoren wenig geeignet. Das gilt insbesondere für mathematische Objekte, zu deren Erzeugung mehr als zwei Zufallszahlen erforderlich sind. Würde man beispielsweise damit versuchen, eine zufällige Punktewolke in einem Würfel zu generieren, so kämen alle Punkte auf zwei Ebenen zu liegen.
Verzögerter Fibonacci-Generator
Das Prinzip des Fibonacci-Generators kann aber verallgemeinert werden, indem man nicht die beiden letzten, sondern weiter zurückliegende Zustandswerte zur Erzeugung der neuen Zufallszahl verwendet. Dies ergibt einen verzögerten (engl. 'lagged') Fibonacci-Generator:
- mit den Startwerten
Dann ist also und , die übrigen sind Null. Dabei wählt man in der Regel gerade und und so, dass das Polynom in
ein primitives Polynom modulo 2 ist. Dann beträgt die Periodenlänge des Generators mindestens .
Die folgende Tabelle gibt einige Wertepaare für und an, die diese Bedingung erfüllen:
| A | 2 | 31 | 55 | 73 | 98 | 100 | 135 | 258 | 607 | 3217 | 23209 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| B | 1 | 13 | 24 | 25 | 27 | 37 | 22 | 83 | 273 | 576 | 9739 |
ist genau dann ein primitives Polynom modulo 2, wenn dies für gilt. Somit kann man statt immer auch verwenden.
Dieser Generator wird auch praktisch eingesetzt. Er liefert aber ebenfalls keine vollkommen zufällig erscheinenden Zahlen. Das Problem des einfachen Fibonacci-Generators wird nur verlagert: Man hat niemals oder . Außerdem gibt es noch weitere Mängel.
Als Abhilfe wurde vorgeschlagen, immer nur aufeinanderfolgende Zahlen zu verwenden, und dann die nächsten bis Zahlen zu verwerfen. Dies funktioniert gut, aber um den Preis eines 5- bis 11-mal höheren Rechenaufwands. Der von Donald Knuth vorgeschlagene Generator ranarray arbeitet auf diese Weise. Bei ihm ist und , und von 1009 aufeinanderfolgenden Zahlen wird immer nur ein Block von 100 Zahlen verwendet.
Um die Periode sicherzustellen, kommt es nur auf das jeweils niederwertigste Bit in den Zustandswerten an, also darauf, ob sie gerade oder ungerade sind. Man kann die höherwertigen Bits beliebig modifizieren, um die Qualität der erhaltenen Zufallszahlen zu verbessern. Beispielsweise:
Andere
Man kann den verzögerten Fibonacci-Generator weiter verallgemeinern, indem man mehr als zwei Zustandswerte verarbeitet:
- .
ist hier das größte Element in . Um eine Periode von mindestens zu garantieren, muss auch hier das entsprechende Polynom
- oder gleichbedeutend das Polynom
ein primitives Polynom modulo 2 sein (mit geradem Modul ). Ein so konstruierter Generator mit liefert im Allgemeinen bessere Zufallszahlen als mit , aber wiederum um den Preis eines höheren Rechenaufwands.
Mit einer weiteren Verallgemeinerung kann man bei gegebenem die Periodenlänge vergrößern und wohl auch die Qualität der Zufallszahlen weiter verbessern. sei ein Primfaktor von . für die Berechnungsvorschrift
werden die derart gewählt, mit , dass das Polynom in
ein primitives Polynom modulo ist. Dann beträgt die Periodenlänge mindestens .
Der vorige Generator ergibt sich daraus mit und als Sonderfall, und liefert einen multiplikativen Kongruenzgenerator mit der Periodenlänge .
Das Polynom ist ein primitives Polynom modulo , wenn die folgenden Bedingungen erfüllt sind:
()
- ist ein primitives Element modulo
- das Polynom ist kongruent zu (modulo )
- für alle Primfaktoren von ist der Grad des Polynoms positiv
Dabei wird Polynomarithmetik angewandt (siehe Polynome sowie Polynomdivision), und mit den Koeffizienten wird modulo gerechnet (sie sind Elemente des Restklassenrings ).
Siehe auch
Einzelnachweise
- ↑ Donald E. Knuth: The Art of Computer Programming. Volume 2: Seminumerical Algorithms. 3. Auflage. Addison-Wesley, 1997, ISBN 0-201-89684-2, S. 10–26
- ↑ Stackoverflow-Forum: Understanding the algorithm of Visual C++'s rand() function
- ↑ Rosetta Code: Linear congruential generator
- ↑ GeeksforGeeks: Linear Congruence method for generating Pseudo Random Numbers
Weblinks
Abhandlung über Bitstrom-Verschlüsselungen





































































































































